El método de Gauss
es una generalización del método de reducción y consiste en transformar el
sistema dado en otro equivalente en el que se haya eliminado el máximo número
de incógnitas y de ecuaciones posible.
Para aplicar el método de Gauss utilizamos todas las
transformaciones ya explicadas:
- Intercambiar dos ecuaciones
- Sustituir una ecuación por ella misma multiplicada o sumada por un número real distinto de 0.
- Sustituir una ecuación por ella misma más un escalar por otra ecuación distinta.
- Despejar una incógnita de una ecuación y sustituir dicha expresión dónde aparezca la incógnita en otra ecuación.
- Eliminar una ecuación con todos los coeficientes 0.
- Eliminar una ecuación que es igual a otra.
- Eliminar una ecuación que sea proporcional.
- Eliminar una ecuación que sea “combinación lineal” de otras.
Lo que conseguimos con este método es encontrar sistemas
equivalentes al inicial cada vez más sencillos al inicial, hasta llegar a uno
que este formado por las propias soluciones del sistema.
*No saldría rentable con un sistema de dos ecuaciones.
- Ejemplo, resuelve el siguiente sistema mediante el método de Gauss:
Resolvemos poniendo el sistema de forma matricial y aplicando las transformaciones ya citadas.
Debemos conseguir hacer ceros los coeficientes que se
encuentran por debajo de la matriz ( la diagonal)
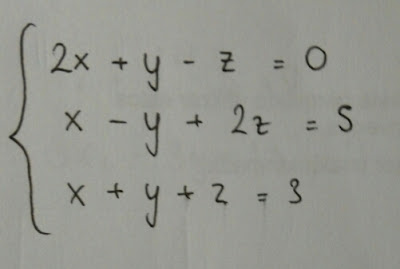



No hay comentarios:
Publicar un comentario