34. Resuelve la ecuación: x⁵ - 5√2 x⁴ + 20x³ - 20√2 x² + 20 - 4√2 = 0
A la hora de realizar este ejercicio me fijo en el 18:
18.- Enuncia el teorema del factor y aplícalo, para
factorizar el polinomio x⁵ - 5√2 x⁴ + 20x³ - 20√2 x² + 20 - 4√2 = 0, sabiendo que √2 es una raíz de multiplicidad 5.
Teorema del factor:
Un polinomio P (x) es divisible es divisible por otro de la forma (x-a) si, y sólo si P(a) = 0, siendo en este último caso º raíz de P(x)
- Para hallar C(x) utilizamos Ruffini:
* Por tanto la solución del ejercicio 34 es x=√2
8. Demuestra que todo número radical es un número algebraico.
Los números algebraicos están por encima de los números radicales puesto que no abarcan únicamente los radicales.
- Un número algebraico es aquel que es solución de un polinomio no nulo con coeficientes racionales.
Ejemplo:
- Del polinomio P(x): x⁵ - 5√2 x⁴ + 20x³ - 20√2 x² + 20 - 4√2 = 0
- Con coeficientes racionales:
- Cuya solución es : x= √2
√2 es un número radical.
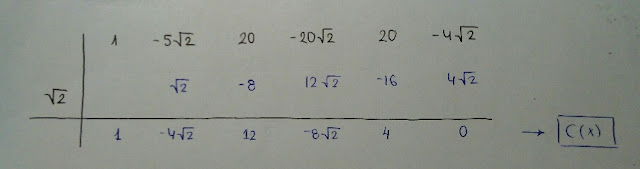
No hay comentarios:
Publicar un comentario